鼓式制動器、摩托車剎車圈、Drum brake、輪轂剎車圈專業生產廠家無錫九環2022年1月25日訊 電動汽車輪轂電動機經常要在復雜的工況和惡劣環境下運行,狹小的安裝空間和較高的密封性要求,使得輪轂電動機經常因為較高的溫升而損壞,所以在輪轂電動機設計初期就必須對其溫升性能進行精確計算與設計,防止輪轂電動機因為溫升過高而損壞。
因為電動汽車用輪轂電動機安裝于空間狹小的電動汽車車輪內部,并且汽車正常行駛的道路路況復雜,所以要求輪轂電動機具有較高的密封性,這樣直接使輪轂電動機的散熱能力較差。同時為了減小汽車懸架的簧下質量,要求電動機具有結構緊湊和高功率密度的性能。但是較高的功率密度會引起較大的工作電流,這樣會使電動機的損耗和溫升較高,不利于輪轂電動機的長期使用。所以,較高溫升和較差的散熱條件,使對輪轂電動機溫升的準確計算顯得愈發的重要。
目前,國內外學者對電動機溫升的計算方法主要有三種方法,即參數計算法、等效熱路法和有限元分析法。其中,國外的Christian Kral等人采用了參數計算法建立了輪轂電動機溫度場計算數學模型,雖然計算速度較快,但是不能真實地反映出電動機內部的溫度分布情況,存在一定誤差;Wang R.J等人采用等效熱路法,計算的結果表明該方法能夠計算出電動機內部的溫度分布,但缺乏試驗驗證,并且熱路法模型的建立較為復雜。
國內賈珍珍等人運用有限元方法分析了輪轂電動機的溫度場分布和溫升情況,但是僅采用了二維平面有限元分析方法,沒有考慮電動機軸向溫度散熱能力對電動機整體溫度的影響;高曉林等人運用Fluent流體分析軟件對電動機的散熱進行了分析,但是Fluent網格劃分要求較高,前處理時間較長,對于復雜的電動機內部結構,不利于實際工程計算中的效率要求。
為了使溫升計算結果較為準確,并且計算效率較高,本文以一臺4kW輪轂電動機為研究對象,以輪轂電動機各部件電磁損耗為熱源,在ANSYS Transient Thermal模塊中分析了額定工況下的輪轂電動機的整體溫度場。根據傳熱學原理,本文提出將輪轂電動機內部復雜結構的求解模型進行簡化和等效處理,并通過相關流體力學的公式,計算出散熱邊界條件來模擬輪轂電動機的散熱情況,最后將得出的輪轂電動機溫度場的仿真數據與試驗數據進行對比,驗證了本文所提出的仿真計算方法的正確性,為輪轂電動機的冷卻結構設計提供重要的理論依據。
輪轂電動機熱性能參數的確定
1. 輪轂電動機的基本參數
輪轂電動機的基本參數見表1。
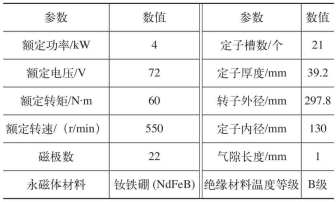
表1 電動機基本參數
電動機內部結構較為復雜,結構較為緊湊,散熱條件較差。在自然風冷條件下,輪轂電動機的主要熱交換方式如圖1所示,其中主要包括電動機內部各部件的傳熱、電動機外部殼體和內部結構的對流換熱等組成。
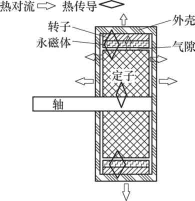
圖1 電動機內熱交換
2. 熱源計算
電磁損耗主要包括定轉子鐵心損耗、銅耗和永磁體渦流損耗,其中電磁損耗是輪轂電動機的主要熱源,因此需要準確地計算出電磁損耗的具體數值。通過Maxwell電磁分析軟件準確地分析出額定工況下輪轂電動機各部件的電磁損耗分布云圖。如圖2a所示,在齒頂處的定子鐵心損耗較大,這是因為此處的磁密度較為集中。如圖3所示,在齒槽開口處的永磁體渦流損耗較大,這是由于槽口存在的齒槽效應會產生磁場高次諧波,會引起較大的渦流損耗。
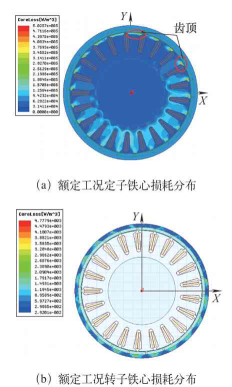
圖2 額定工況定子和轉子鐵心損耗分布
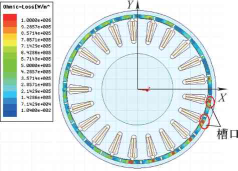
圖3 額定工況永磁體渦流損耗分布
經過Maxwell后處理計算模塊,得到輪轂電動機定子、轉子鐵心損耗和永磁體渦流損耗具體數值大小,見表2。其中,電動機繞組銅耗可以通過傳統的測電阻并用公式計算的方法得到。轉子的鐵耗較小,僅為定子鐵耗的0.89%,可以忽略不計;銅耗的數值最大,占整體電磁損耗的一半。

表2 額定工況下電動機內各部件的電磁損耗分布(%)
輪轂電動機溫度場分析
1. 復雜部件的簡化與等效
(1)定子槽繞組模型的簡化與等效。在建立溫度場分析模型時,定子槽中的繞組和絕緣體結構復雜,很難對其進行精確建模和導熱系數的計算,可以將繞組等效為一整快導體,絕緣體按體積等效成等體積的包圍層,并平行緊貼于槽壁,簡化模型如圖4所示。
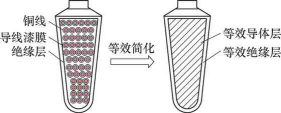
圖4 定子槽繞組模型等效簡化
根據傳熱學定理,通過相關公式得到等效后的絕緣層和導體的物性參數,計算得到等效絕緣體的等效結構尺寸和等效物性參數,見表3。
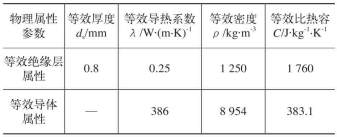
表3 定子槽繞組等效模型的等效物性參數
(2)鐵心疊片模型的等效與簡化處理。定子鐵心是由多層硅鋼片經過疊壓而成的,結構比較復雜。根據傳熱學定理,可以將鐵心疊片等效成具有軸向、周向和切向不同導熱性能的結合體。
可以通過公式計算得到定子鐵心在各個方向上的導熱系數。
通過計算得到等效模型物理屬性參數見表4。

表4 定子鐵心簡化模型物理屬性參數
(3)輪轂電動機其他部件的等效與簡化。為了使溫度場分析時的有限元模型較易求解,所以對輪轂電動機中溫度場分析影響較小的次要部分進行一定的省略和簡化,主要體現在幾個方面:忽略對整體模型影響較小的小尺寸零件,如螺栓、墊片等;忽略電動機外殼的兩邊端蓋,以等效散熱系數等效兩邊端蓋的散熱作用,保留與電動機轉子相接觸的頂部外殼;假設電動機內部有裝配關系的零件是相互接觸緊密、無空隙的。
對輪轂電動機實際結構進行簡化與等效處理后得到的簡化模型,如圖5所示。
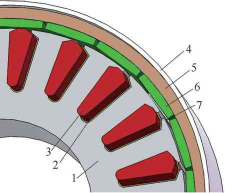
圖5 輪轂電動機簡化模型
2. 對流換熱系數的等效與計算
輪轂電動機主要的對流換熱邊界面為機殼外表面、機殼端面、轉子端面、轉子內表面、永磁體端面、氣隙端面、繞組端部內表面、繞組端部外表面和定子端面。
(1)氣隙散熱系數的計算。隨著電動機轉子的旋轉,電動機氣隙中的空氣會流動,由于氣隙的尺寸較小,很難在溫度場計算時模擬氣隙的旋轉和運動,因此對定轉子間的氣隙做靜止處理。
(2)輪轂電動機外殼表面散熱系數的計算。電動機殼在旋轉時通過對流的形式與外界環境發生熱交換,同時旋轉電動機的外殼會加速周圍空氣的流動從而增強散熱效果。
通過公式計算得到電動機對流散熱邊界面的散熱系數,具體數值見表5。

表5 輪轂電動機各邊界面對流散熱系數 (單位:W/m2·K)
額定工況下輪轂電動機溫度場仿真結果分析
進行瞬態溫度場求解后,得到額定工況下的輪轂電動機運行3 600s時的最高溫升變化曲線,如圖6所示。電動機的最高溫升隨時間成遞增趨勢,在前半段電動機的溫升速率較快,在后半段逐漸趨于穩定,在3 600s時的最高溫度為122.23℃,最高溫升為99.747℃。樣機的絕緣材料耐溫等級為B級,即最高允許溫度為130℃,所以電動機在額定工況下連續工作1h時間是安全可靠的。
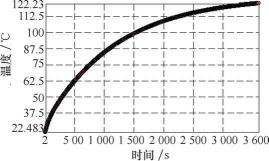
圖6 額定工況下的電動機溫升變化曲線
整體溫度分布云圖和各部件的溫度分布云圖,如圖7所示。從溫度場仿真結果可知,繞組部分的溫度最高,這和損耗分析時繞組是電動機中最大熱源的結果一致:繞組最高溫度為122.23℃,最低溫度為121.45℃。由于槽絕緣的隔熱作用,繞組的最高溫度區域出現在繞組中間位置,最低溫度區域出現在兩端,但是繞組的溫度差異較小,整體溫度分布較為均勻。
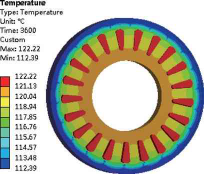
圖7 電動機整體溫度分布
定子的最高溫度區域出現在槽底部與定子軛內圓之間的位置,因為定子的位置與繞組位置最接近,并且定子本身也是發熱源,所以定子的最高溫度僅次于繞組,最高溫度為120.78℃。
永磁體的溫差較大,最高溫度為118.22℃,最低溫度為113.24℃。由于磁極內圓處接近溫度較高的定子,外圓接近散熱較好的轉子與外殼,所以磁極內圓與外圓形成了一個4.98℃的溫差范圍。
試驗驗證
為了驗證本文輪轂電動機溫度場仿真方法的正確性,需要對輪轂電動機進行溫升試驗。運用溫度傳感器埋入繞組端部,以檢測端部溫度變化,并運用紅外溫度計測量電動機外殼溫度。試驗所用的檢測平臺為輪轂電動機綜合性能試驗臺,該試驗臺由測功儀、控制器、試驗架、溫度傳感器等部件組成。
為了減小試驗值和仿真值的對比誤差,則需要使試驗條件和仿真條件基本相同,控制實驗室初始環境溫度為22℃。在試驗過程中運用測功儀和控制器配合,使輪轂電動機在額定負載工況下連續平穩運行1h,并以5min為時間段記錄溫度數據。將得到的溫升試驗結果與仿真結果進行對比,對比曲線如圖8所示。
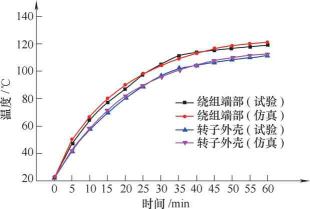
圖8 輪轂電動機溫度試驗與仿真對比曲線
由圖8輪轂電動機溫升試驗與仿真的對比曲線可知,轉子外殼的仿真結果與試驗結果幾乎一致,誤差在2%以內。繞組端部的仿真誤差較大,最終穩定時的誤差相差約2.2,但整體誤差在5%以下,該結果在工程計算的誤差允許范圍內。所以與通過試驗結果的比對,驗證了本文采用的磁-熱耦合仿真計算輪轂電動機溫度場的方法的正確性,同時也驗證了該方法能夠運用于電動機初期設計中,并且能為輪轂電動機散熱結構的設計提供重要的參考依據。
結 語
本文通過磁熱耦合的方法,對一臺4kW電動汽車用輪轂電動機的溫度場進行了研究,得出以下結論:
1)通過將輪轂電動機溫度場的仿真結果和試驗結果進行對比,驗證了本文用電磁損耗為熱源和散熱系數相結合的磁熱耦合分析方法的正確性。
2)仿真誤差低于5%,驗證了本文運用簡化模型和散熱邊界條件計算方法的正確性。該方法能夠有效增加求解速度,并保證求解精度。
3)本文采用的磁熱耦合分析的方法,能夠快速準確得到輪轂電動機各部件的溫度場分布情況,能夠為輪轂電動機冷卻結構的設計提供重要的參考依據。





