51国产福利视频在线观看,www.精品国产,99久久综合狠狠综合久久一区

信息中心

基于復特征值分析的某盤式制動器制動尖叫問題改進

摘要：鼓式制動器、摩托車剎車圈、Drum brake、輪轂剎車圈專業生產廠家無錫九環2022年3月25日訊 以某車型出現2 000 Hz制動尖叫問題的盤式制動器為研究對象，建立制動器的有限元模型。通過試驗模態對有限元模型進行修正，應用復特征值分析技術，獲取系統的復特征值和振型，并通過ODS測試確認與制動尖叫頻率對應的不穩定模態。然后針對此不穩定模態，通過相關性分析量化制動器零件對系統不穩定模態的貢獻，采用優化具有最大貢獻量的零件幾何結構來改善制動尖叫。最后通過SAE J2521臺架試驗驗證此方法可行。

制動器在不斷滿足和提高產品功能性的同時，出于駕駛和乘坐舒適性的考慮，制動噪聲問題日益被消費者所關注。對于汽車制造商，制動噪音問題會增加大量的售后成本并降低客戶對汽車質量和可靠性的認可度，因此制動噪聲已成為汽車制造商亟待解決的一個重要問題。汽車制動噪音的發生受溫度、濕度、制動壓力、車速等眾多因素的影響，具有很大的隨機性，頻率覆蓋廣泛，如頻率在1 000 Hz以下的起步咕音(Groan)、咯吱音和Moan音，頻率在1 000 Hz以上的制動尖叫(squeal)，且其發生機理復雜，涉及摩擦學、振動力學等眾多學科，對其的研究從發生機理到分析方法仍未取得一致結論，也沒有形成完善的工程控制手段。

本文針對某車型盤式制動器在低速蠕行工況下出現2 000 Hz制動尖叫問題進行研究，如圖1所示，按照SAE J2521規范中的程序,對此制動器在臺架上進行噪音搜索試驗，在低速低壓工況集中復現了2 000 Hz制動尖叫，噪音搜索結果如圖2所示。

圖1 制動器臺架試驗
Fig.1 Brake bench test

工程上目前在解決制動尖叫類問題時，一般通過摩擦片和消音片的預選以及制動噪音匹配試驗的方式來應對，即通過調整摩擦片的開槽、倒角、配方及消音片的阻尼特性，然后在試驗臺上進行噪音搜索來驗證改善效果。有限元復特征值分析方法的提出，逐步成為工程上解決或抑制制動尖叫問題的另一有效方法，通過有限元計算提取制動器的復特征值和模態振型，利用特征值的實部或阻尼比來分析系統是否不穩定并判斷尖叫發生的傾向。本文即采用有限元復特征值分析方法，結合試驗模態及多普勒激光測振手段，基于復特征值及相關性分析的結果調整制動器零件的幾何結構，消除了2 000 Hz制動尖叫。

圖2 制動器臺架噪音搜索試驗結果
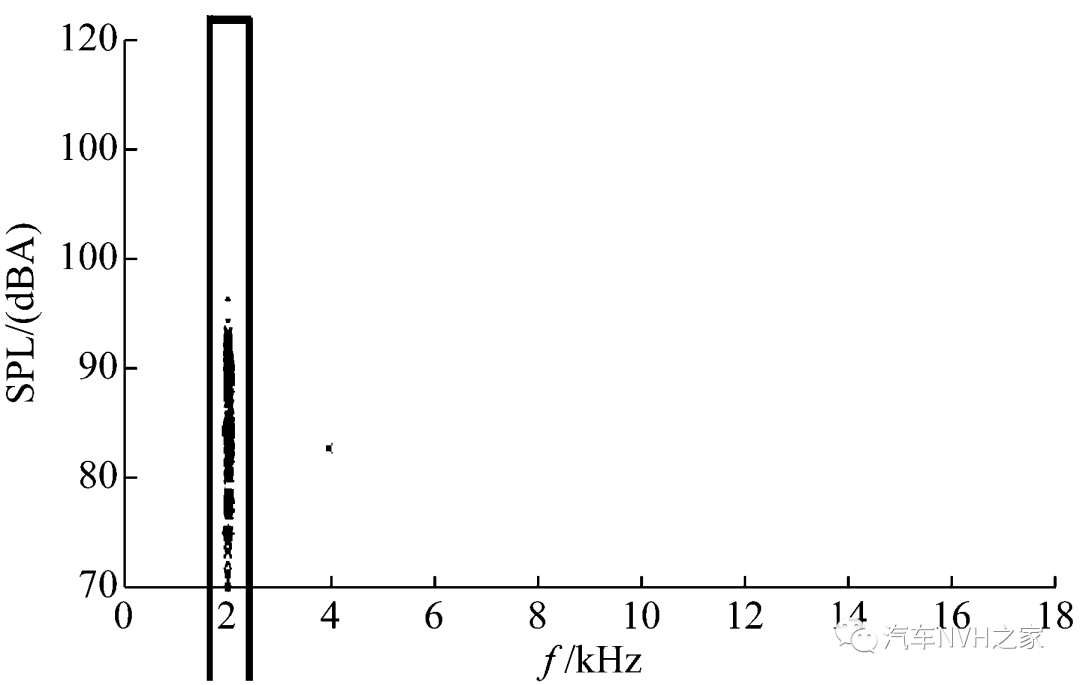
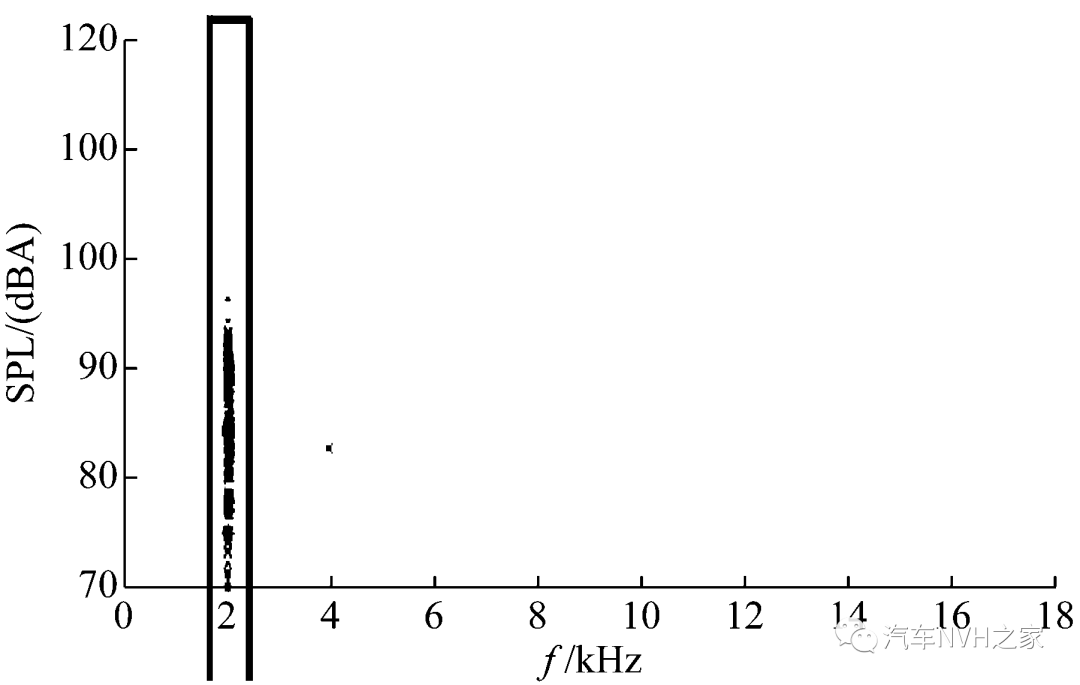
Fig.2 Results of noise in brake bench test

1 復特征值分析理論

復特征值分析基于模態耦合理論，制動盤和摩擦片之間的盤片耦合相當于在系統上提供了一個擾動載荷，它會將導致系統剛度矩陣的不對稱，將系統的不穩定模態激勵起來。通過對復特征值問題的求解，確定系統中哪些模態是不穩定的，容易發生自激和尖叫。

考慮系統制動時制動盤與摩擦片之間的摩擦力，系統的動力學方程如下

(1)

式中:M、C、K分別為系統的質量矩陣、阻尼矩陣和剛度矩陣，u為系統的各自由度的位移向量；Ff為制動盤與摩擦片之間的接觸摩擦力，它以接觸面之間節點的相對位移來表示為

{Ff}=[Kf]{u}

(2)

這個將摩擦力與節點位移聯系起來的矩陣稱為摩擦剛度矩陣，或者簡稱為摩擦矩陣。

結合式(1)和(2),將式(1)中的摩擦力從右邊移到左邊可寫成如下二階齊次線性微分方程形式

(3)

式(3)是包含了摩擦剛度項的自由振動系統的動力學方程，其解的形式如下

u={Φ}est

(4)

將其進行適當的微分并代入式(3)得到

([M]s2+[C]s+[K-Kf]){Φ}={0}

(5)

式中:Φ為特征向量，s為特征值。不同于系統中慣性力和彈性力導致的對稱質量矩陣和剛度矩陣，摩擦力導致的摩擦矩陣Kf是不對稱的，它會導致系統的剛度矩陣不對稱。剛度矩陣不對稱在一定條件下會求解得到如下包括實部和虛部的共軛復特征值

si1,2=σi±jωi

(6)

系統的運動可以用共軛復特征值和特征向量來描述

{ui}={Φi}e(σi+jωi)t+{Φi}e(σi-jωi)t

(7)

通過歐拉公式變換可以得到

{ui}={Φi}eσitcos ωit

(8)

對于第i階模態，σi是其特征值實部，代表系統的阻尼系數，ωi是其虛部，代表系統的阻尼固有頻率。正的實部會使振動擴大，發展為強烈的自激振動，此時系統是不穩定的，因而通過對系統特征值實部的分析，可以確認系統中不穩定且容易產生制動尖叫的模態。

2 制動器有限元復特征值分析

2.1 盤式制動器有限元模型

盤式制動器系統有限元模型包括制動盤、卡鉗本體、卡鉗支架、導向銷、內/外制動背板、內/外消音片、活塞、內/外摩擦片以及對手件輪轂軸承、軸節。在Hypermesh中進行幾何清理，采用四面體單元劃分網格，結合制動器各零件結構和工作原理，采用綁定、接觸、剛性連接等方式定義各零件之間的連接關系，裝配后形成完整的制動器有限元網格模型如圖3所示。

圖3 盤式制動器有限元模型
Fig.3 FEA model of disc brake

2.2 零部件材料屬性定義

定義摩擦片為橫觀各向同性材料，其屬性采用實測值進行設置，摩擦片材料參數如表1所示。

表1 摩擦片材料參數

Tab.1 Parameters of friction materials

各零部件通過稱重、試驗模態進行修正有限元模型中的材料密度和彈性模量，修正后使各零部件的自由模態計算結果與試驗模態結果誤差在3%以內。以制動盤為例，圖4為其模態測試試驗。

圖4 制動盤模態測試
Fig.4 Modal test of brake disc

表2為其修正材料參數后試驗與計算模態頻率的對比。

表2 制動盤試驗與計算自由模態頻率對比

Tab.2 Comparison of brake disc modal frequency between test and FEA analysis at free-free condition

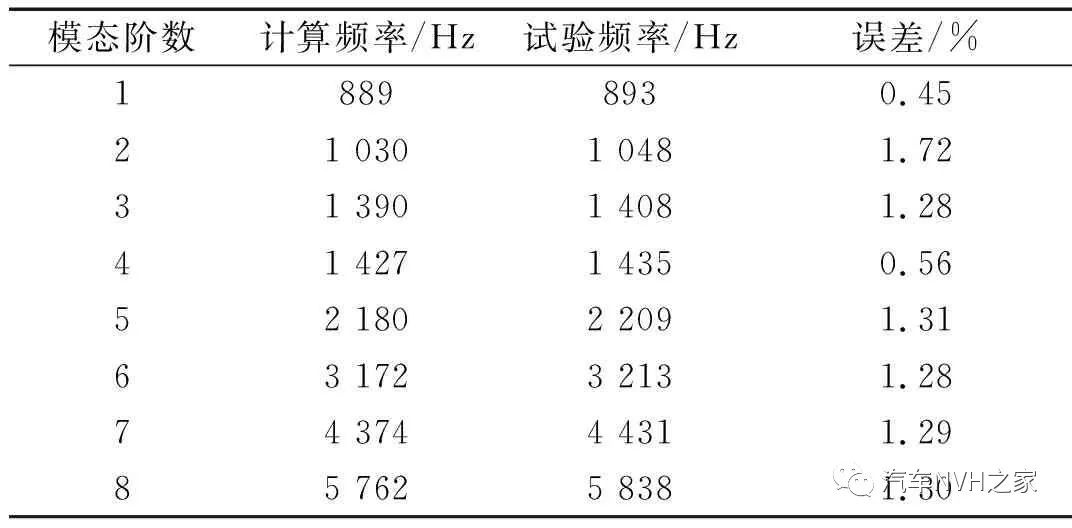
2.3 盤式制動器有限元模型

卡鉗支架與轉向節之間通過螺栓連接，需對此連接螺栓添加預緊力，轉向節和制動盤通過螺栓連接在輪轂軸承的兩側，約束轉向節與懸架連接各點的6向自由度，考慮到制動尖叫出現在低速低壓工況，一方面需在活塞和卡鉗油缸底部施加相應的制動壓力，另一方面需對制動盤添加轉動效應。制動油壓和旋轉速度分布如表3，共20個工況進行復特征值的求解。

表3 復特征值分析各工況制動壓力

Tab.3 Brake pressure in complex eigenvalue analysis

2.4 復特征值分析結果

使用ABAQUS軟件提取5 000 Hz以內的盤式制動器復模態結果，如圖5，以散點圖方式繪制出各工況下出現的不穩定模態的特征值實部和頻率的信息。圖中的1 900 Hz不穩定模態頻率出現的工況次數最多，阻尼系數相對偏高且集中，說明其發生制動尖叫的傾向性較大，同時它與臺架噪音搜索結果出現的2 000 Hz的噪聲頻率非常接近。

圖5 盤式制動器復模態分析結果
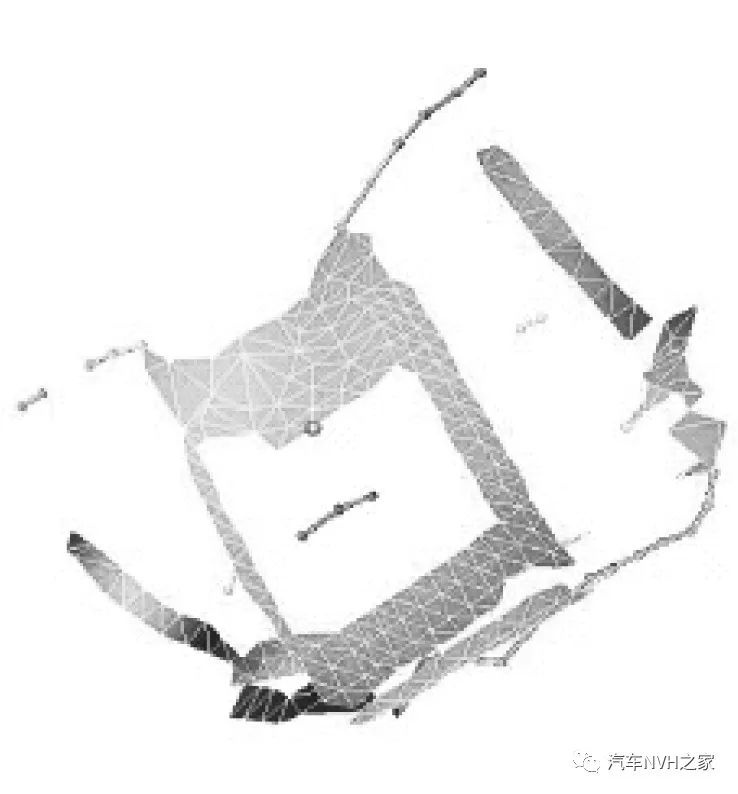
Fig.5 Results of complex eigenvalue analysis

在臺架上進行噪音復現的同時，配合三維掃描式多普特激光測振儀，測試系統在2 000 Hz制動尖叫出現時的ODS振型，如圖6所示，與復模態仿真分析結果中的1 900 Hz不穩定模態進行對比，確認二者振型是吻合的。因而，可以確認復特征值分析中的1 900 Hz不穩定模態與實際發生噪音模態一致。

(a) ODS測試結果
鼓式制動器,摩托車剎車圈,輪轂剎車圈,Drum brake,摩托車制動鐵套

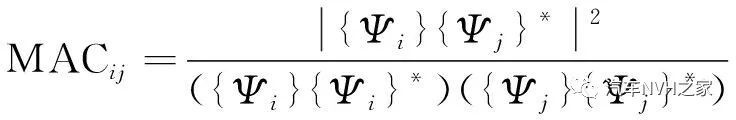
(b) 不穩定模態振型
圖6 ODS測試與不穩定模態分析結果對比
Fig.6 Comparison of ODS test with unstable modal of FEA

各工況出現的不穩定模態中，在650 Hz、2 300 Hz、2 550 Hz頻率處也相對比較集中，但實車中并未出現該頻率的噪音，這代表仿真結果出現了“過預測”。為了找到與臺架上復現的制動尖叫所對應的的不穩定模態，“過預測”現象在本文中是希望出現的。出現“過預測”，原因為對制動盤和摩擦片之間設置了較大的摩擦因數，激勵了更多的不穩定模態，且沒有考慮摩擦所誘導的阻尼及結構阻尼，阻尼對不穩定模態的出現是有抑制作用的。

3 子零件模態貢獻量分析

針對上文已經確認的不穩定模態，通過相關性分析找出與其相關程度較高的實模態，然后統計這些相關程度較高的實模態的應變能信息來量化制動器零件對系統不穩定模態的貢獻，據此找到具有最大貢獻量的部件，為后續對子零件進行結構優化工作提供依據和指導。

3.1 相關性分析

采用模態置信因子(MAC)來對復模態與實模態進行比較，MAC表示一對向量之間的相關程度，這一對向量可以是復模態向量、實模態向量或者是外界激勵工況下的響應向量，通過MAC可以識別出兩個在一定摩擦激勵下能夠發生耦合的實模態。其表達式為

(9)

式中:Ψi、Ψj分別為實模態、復模態各階模態的振型向量，MACij為第i階實模態與第j階復模態之間的相關程度，它的值介于0～1之間，包含了幅值和相位的信息。根據前文所建立的有限元模型，提取系統前5 000 Hz的復模態與實模態各階模態振型向量，得到系統各階復模態與實模態的MAC矩陣。針對1 900 Hz(第36階)的不穩定模態，提取它與各階實模態的部分MAC值如表4所示，排名前二的第35、36階實模態與它的相關性為47%、57%，代表了這兩階模態是1 900 Hz不穩定模態的主要參與者。

表4 系統復模態與實模態的MAC

Tab.4 MAC between 36th complex mode and real modes

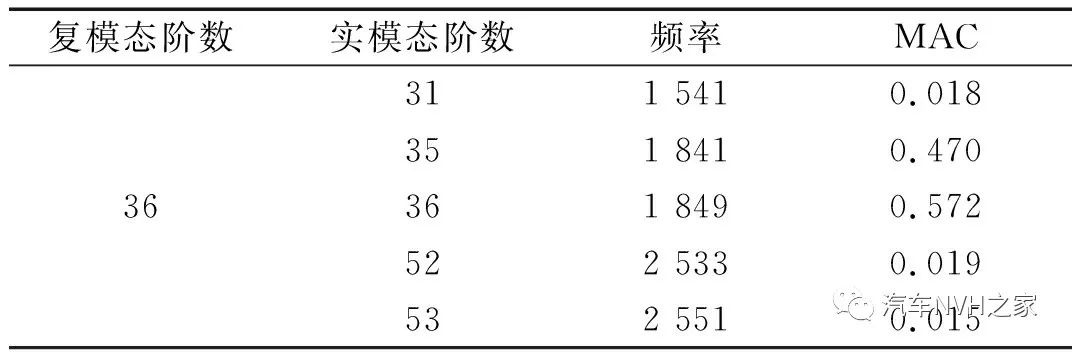
3.2 子零件模態貢獻量分析

應變能能很好地反映一個子零件對整個系統的貢獻，在模態分析中，第i階模態的第j單元的模態應變能(MSE)定義為

MSEij={Φi}T[Kj]{Φi}

(10)

式中:{Φi}為第i階模態的振型;[Kj]為j單元剛度矩陣。

針對這兩個相關程度最高的實模態，如表5，統計各子零件的應變能信息，結合它們的MAC值進行加權，得到子零件對整個系統不穩態的貢獻量，可以看出卡鉗支架、卡鉗、制動盤主要參與了系統不穩定模態，卡鉗支架具有最高的應變能，說明它對系統的貢獻是最大的。

表5 子零件應變能

Tab.5 Strain energy of subcomponents

針對卡鉗支架，計算其自由模態與系統第35、36階系統實模態的MAC值如表6所示，可以看出支架的第1、3、4、6階自由模態最主要的參與了系統的不穩定模態。

表6 第35、36階系統實模態與支架的MAC值

Tab.6 MAC between bracket free modes and real system 35th and 36th mode

支架的不穩定模態及與其相關程度較高的自由模態如圖7所示。

圖7 36th不穩定模態中支架振型與其相關程度較高的
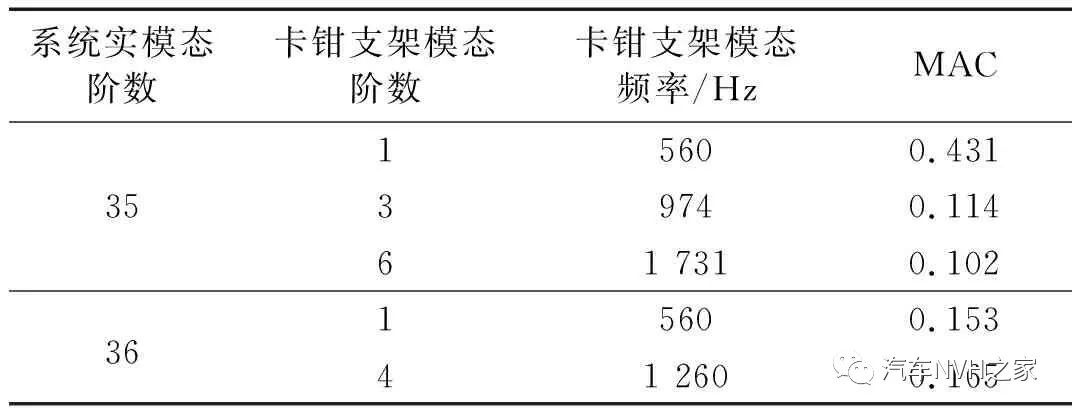
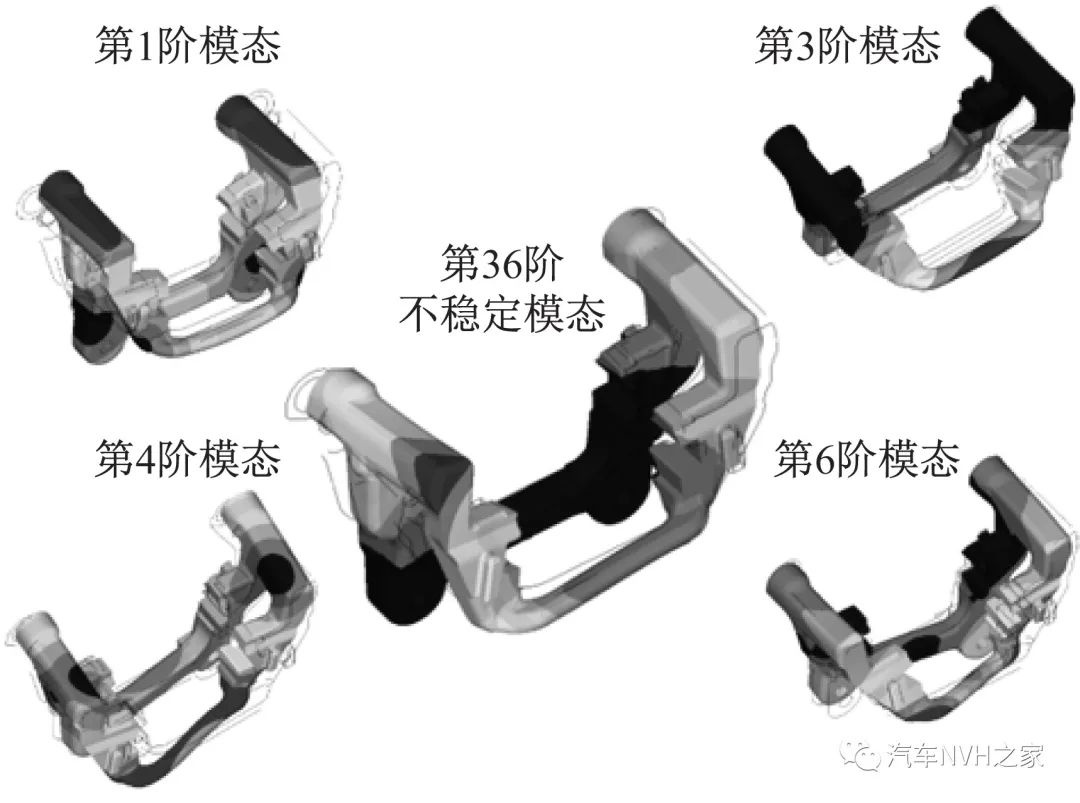
自由模態振型的對比

Fig.7 Comparison of the bracket modal shape between 36th unstable mode and the free modes with high MAC

4 制動尖叫問題改進

確認了支架的自由模態在系統不穩定模態中貢獻量后，可以由圖7中觀察到支架的第1、3、4、6階模態振型都表現為支架外端面梁的振動，對比同平臺其他車型卡鉗支架外端面梁的尺寸，發現此梁相對較細，剛度較弱，如圖8所示，本文考慮通過增加支架外端面梁的厚度來提高支架的剛度，期望達到消除系統不穩定性的目的。

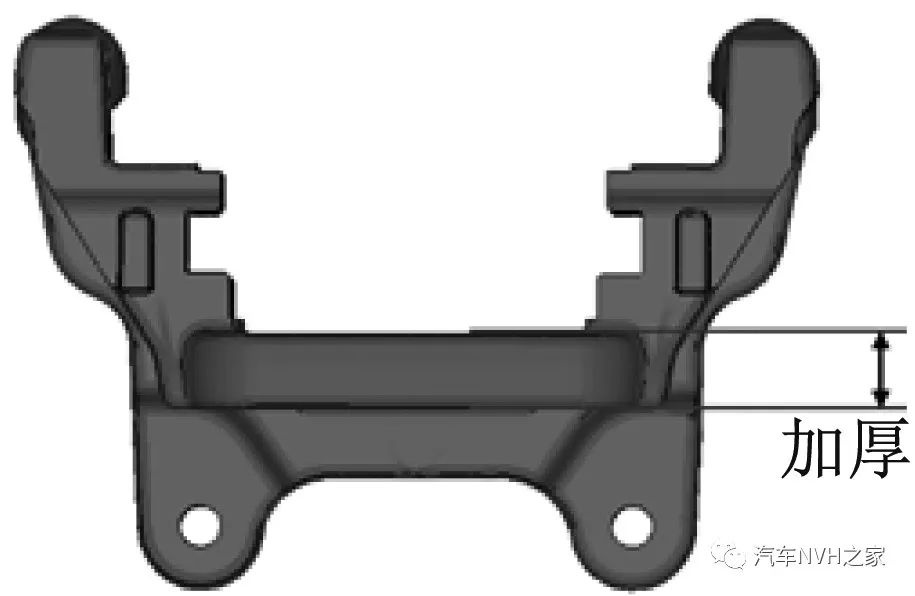
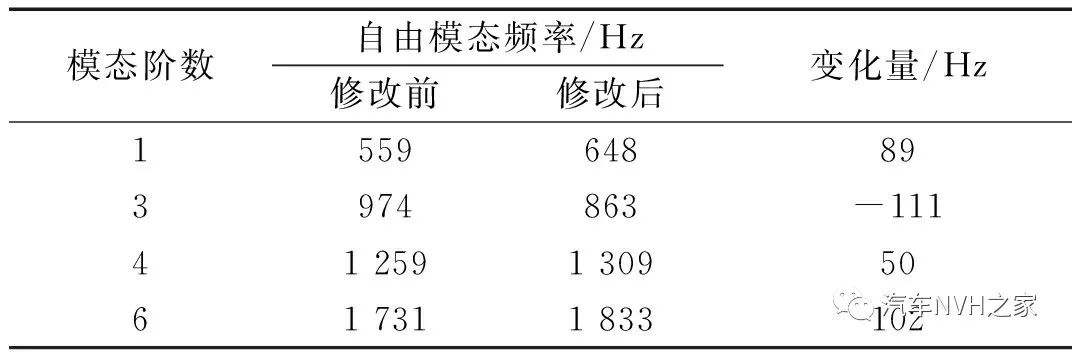
圖8 卡鉗支架的優化方案
Fig.8 Modification of caliper bracket

支架修改前后其第1、3、4、6階自由模態頻率變化情況如表7所示。

表7 支架修改前后模態頻率對比

Tab.7 Comparison of modal frequencies before and after modifying caliper bracket

針對修改支架后的方案進行有限元復模態分析，其仿真結果如圖9所示。

圖9 修改支架后盤式制動器復模態分析結果
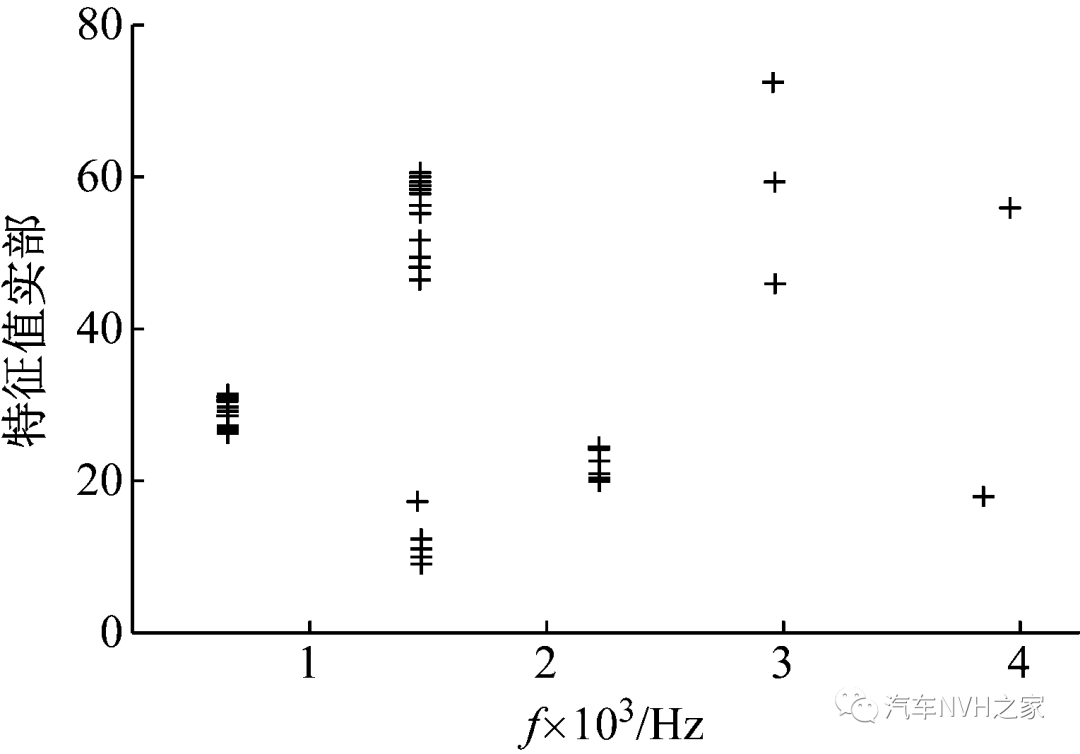
Fig.9 Results of complex eigenvalue analysis after modifying the caliper bracket

從圖9的CAE分析結果可以看出，原方案中集中在1 900 Hz的不穩定模態得到了消除，但新出現了1 500 Hz的不穩定模態。對于CAE分析結果中新出現的1 500 Hz的不穩定模態，考慮到以往實車上并未出現過1 500 Hz噪聲問題，且其振型已不具有原噪聲模態振型的特征，如圖10，對新方案在臺架上進行噪音搜索，未發現1 500 Hz和2 000 Hz的噪音問題，可以說明1 500 Hz不穩定模態屬于“過預測”，修改支架的方案對改進2 000 Hz制動尖叫問題是有效的，因此可以推進此方案實車驗證。

圖10 修改支架后制動器臺架噪音搜索試驗結果
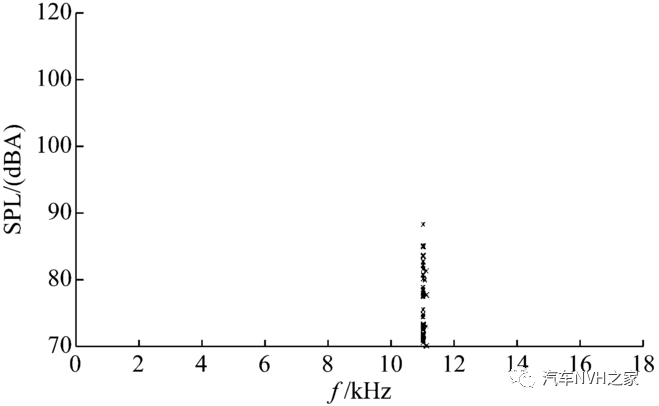
Fig.10 Results of noise in brake bench test after modifying bracket

對于臺架新出現的11 kHz附近噪音，按照復特征值分析方法，如欲將其消除，應重復以上分析過程，直至得到全面理想的抑噪效果[13]。但考慮到11 kHz噪音分貝值相對較低，且改進過程應充分考慮開發周期及試驗成本，同時借鑒前期的開發經驗，不同于 1 500～4 000 Hz的中低頻制動尖叫應對措施，此11 kHz制動尖叫可通過調整消音片的阻尼特性及摩擦片的開槽倒角來快速匹配抑制，對這一噪音匹配過程，本文不作進一步論述。

5 結論

(1) 利用有限元法建模及復特征值分析方法提取系統的不穩定模態，通過與出現制動尖叫時的ODS測試結果進行對比，確認對應的不穩定模態。

(2) 通過相關性分析找出與不穩定模態相關程度較高的實模態，然后統計這些相關程度較高的實模態的應變能信息來量化制動器子零件對系統不穩定模態的貢獻，據此找到具有最大貢獻量的部件。

(3) 通過優化具有最大貢獻量的子零件結構，改變其模態，消除了對應2 000 Hz制動尖叫的系統不穩定模態，且臺架驗證未出現2 000 Hz噪音，說明了復特征值分析方法對于改善制動尖叫的可行性和有效性。

作者：詹斌，孫濤，沈炎武，余家皓，陶政，胡浩炬

廣州汽車集團股份有限公司汽車工程研究院

Previous：KDS 鼓式制動器維護調整指引
Next：某MPV后鼓式制動器制動噪音優化

產品搜索

	?2010-2015 無錫九環機械制造有限公司 All Rights Reserved 電話：13400008068 傳真：0510-88792045
	無錫九環機械專業生產摩托車剎車圈，輪轂剎車圈，鼓式制動器，Drum brake，摩托車制動鐵套，歡迎新老客戶惠顧！網站地圖蘇ICP備20029454號-1
	友情鏈接：天津辦公家具橡膠密封件北京畫室鋼材卷染機牛股推薦標準氣體畫冊制作

<th id="i4soq"></th>

<strike id="i4soq"></strike>

一级黄毛片_被性工具调教的女人电影 _88国产经典欧美一区二区三区 _69xxⅹ色视频免费看

信息中心

信息中心

1 復特征值分析理論

2 制動器有限元復特征值分析

2.1 盤式制動器有限元模型

2.2 零部件材料屬性定義

2.3 盤式制動器有限元模型

2.4 復特征值分析結果

3 子零件模態貢獻量分析

3.1 相關性分析

3.2 子零件模態貢獻量分析

4 制動尖叫問題改進

5 結 論

5 結論