信息中心


鼓式制動器、摩托車剎車圈、輪轂剎車圈專業生產廠家無錫九環2020年7月18日訊 針對某車型由于后制動鼓切向和縱向模態耦合導致的高頻噪音問題,通過對制動鼓幾何形狀及尺寸的敏感度分析,探索其對制動鼓切向和縱向模態隔離的優化方向。首先建立了制動鼓ANSYS 有限元模型,并利用試驗結果驗證模型可靠性,然后通過DOE 試驗矩陣分析方法,得出制動鼓主要幾何參數與模態隔離的敏感度關系,最后通過試驗對模態隔離和參數敏感度分析結果進行驗證。結果表明:基于敏感度分析結果,通過優化制動鼓的關鍵影響因子,可以有效地提高制動鼓的模態隔離結果。
前言
在汽車制動系統中,制動噪音因響度大、發生頻率高、機理復雜、控制難而成為該行業的研究熱點。制動噪音的頻率范圍較大,一般在1000~16000Hz[1-2]。制動鼓是鼓式制動器的關鍵安全部件,是制動系統中最主要的噪音輻射體,其結構振動模態特性是制動噪聲水平的關鍵決定因素,會影響整車的安全性、舒適性、操縱穩定性等基本性能。制動鼓的結構模態優化是解決制動噪音的一種有效途徑[3-6]。模態特性包括固有頻率、阻尼和模態振型,頻率和振型是結構系統承受動態載荷結構設計時的重要參數,這些動力學參數可通過有限元模態分析和試驗模態分析來得到。本文以某轎車的后制動鼓為研究對象,基于有限元模態分析方法,通過改變制動鼓幾何尺寸參數來優化制動鼓切向和縱向模態,并探索制動鼓幾何參數與其模態頻率的敏感度關系,最后,通過試驗模態分析結果對有限元模態分析結果進行驗證,這對優化制動鼓結構設計及縮短設計周期提供了一定的參考,有效縮短設計過程并節省試制和試驗成本。
1 制動鼓參數化模型建立
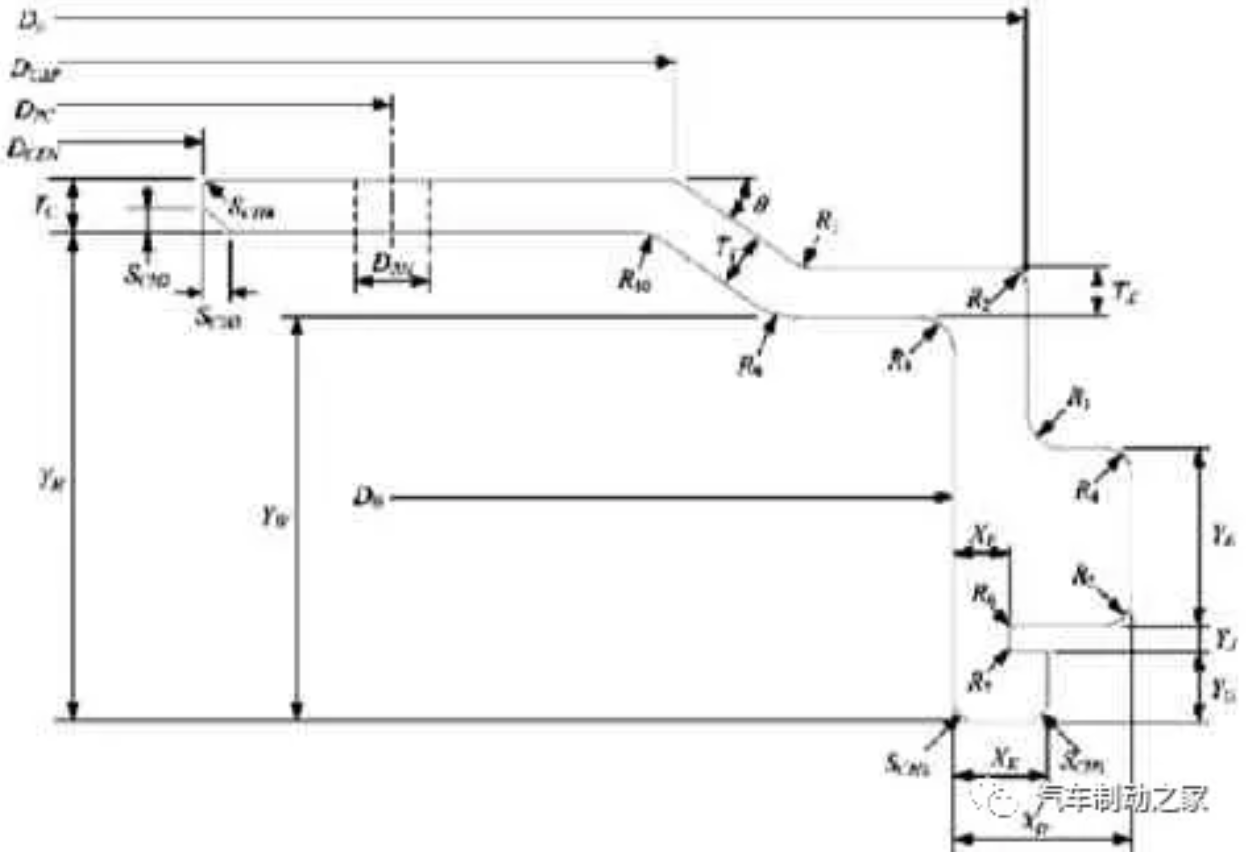
利用UG 軟件建立制動鼓3D 實體模型,然后利用單元劃分軟件進行網格劃分,將劃分好網格的有限元模型導入ANSYS 中進行結構模態分析。圖1(a)為所分析制動鼓實物,圖1(b)為制動鼓的3D 幾何模型,圖1(c)為制動鼓有限元網格劃分圖。制動鼓參數定義如圖2 所示,相應參數值如表1 所示,制動鼓的材料屬性如表2 所示。有限元模型的單元類型為Hex 8 Solid 單元,Hex 8 Solid 單元是一個3D實體結構單元,網格平均長度為3mm,網格數量共36566 個,共47173 個節點。
2 制動鼓參數化模型可靠性分析
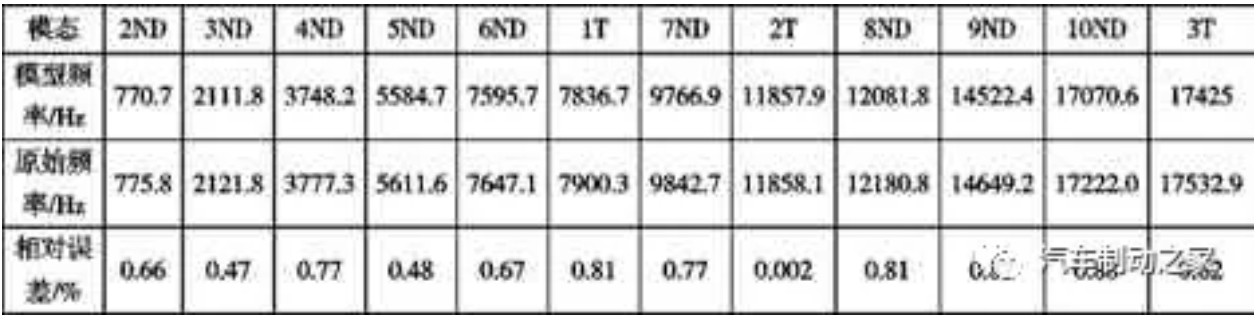
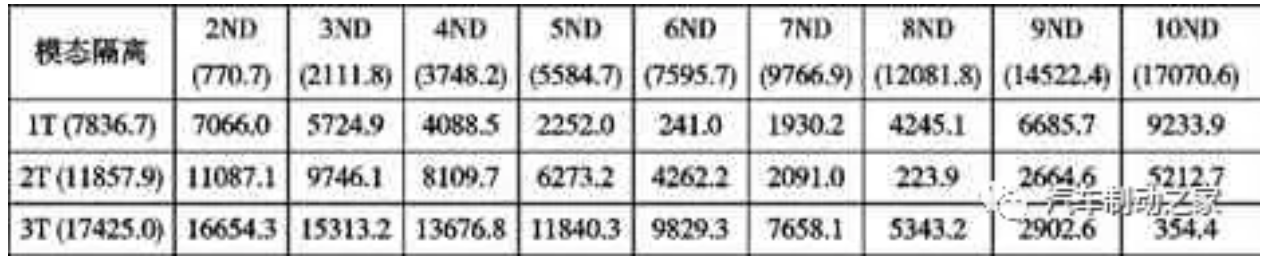
制動鼓自身有多階共振頻率,從而組成一系列離散的頻率譜,即模態是一個頻譜,是由物體的各階共振頻率組成的。隨著振動頻率的升高,振幅隨之減小,影響也有所減小[9]。因此模態分析中前幾階的模態特性最為重要。而且,制動噪音頻率范圍一般在1000~16000Hz,因此通過ANSYS 進行模態分析時提取前 10 階徑向(ND)及前3 階切向(T)模態頻率,滿足涵蓋關注頻率范圍的需求。將該模型的模態分析結果與該制動鼓實物的模態試驗結果進行對比,結果如表3所示。從表3 可以看出,該參數化有限元模型所計算出的前10 階徑向模態及前3 階切向模態頻率與制動鼓實物模態試驗頻率的相對誤差均小于1%,最大誤差僅為0.88%,因此,可認為所建立有限元模型具有較高可靠性和有效性。表4 為該有限元模型的各階切向模態與各階徑向模態之頻率差值|fND-fT|,可以看出該模型能夠將切向模態與徑向模態隔離至200Hz 以上,最小的模態隔離發生在6ND 與1T 以及8ND 與2T 之間,分別為241Hz 和223.9Hz,可以有效地避免產生頻率共振。表3 制動鼓參數化模型模態分析結果與原始頻率之比較
3 制動鼓參數敏感度分析
3.1 制動鼓參數敏感度的確定
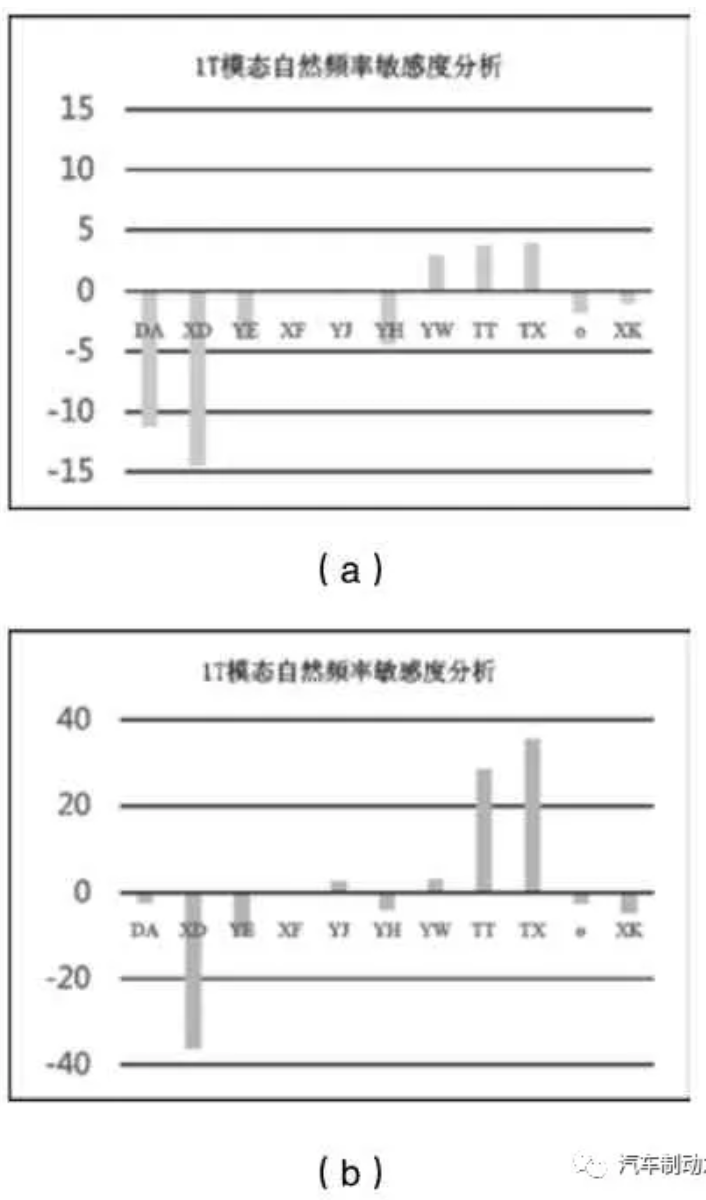
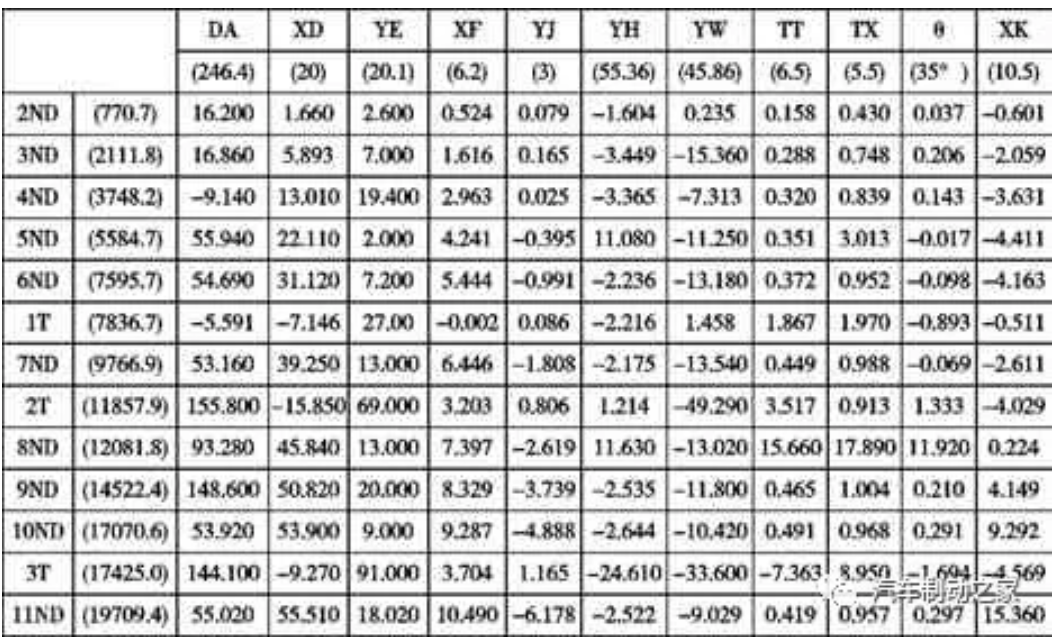
實際零件開發過程中,制動鼓的內徑DB 和安裝面厚度TC 在設計階段就已經是確定的值,一般不可變更。因此在制動鼓模型中,選擇表1 中除了DB 和TC 外的11 個幾何尺寸參數作為輸入變量,將分析結果1T~3T、2ND~11ND 共13個模態頻率作為輸出變量。研究制動鼓模態特性對幾何特征參數的敏感度,共可獲得143 組敏感度值。定義某一輸出變量F 相對于輸入變量Xi 的敏感度為:若輸出變量為正值,則說明該模態頻率與該幾何參數成正相關;若輸出變量為負值,則說明該模態頻率與該幾何參數為負相關。圖3(a)為1T 切向模態頻率相對于11 個輸入變量在-1%~+1%范圍內變化時的敏感度分析結果。從圖3 可以看出,1T 切向模態敏感度與輸入變量防水槽YJ、工作面寬度YW、帽蓋厚度TT 和TX 成正相關,與剩余輸入變量DA、XD、YE、XF、YH、θ、XK 成負相關。從下圖可以看出當DA 從-1%~+1%變化時,即DA 變化量為4.928mm 時,模態頻率變化僅為11.2Hz。而XD、YE、TT、TX 從-1%~+1%變化時,即他們的變化量分別為0.40mm、0.402mm、0.13mm、0.11mm 時,模態頻率變化分別為14.5Hz、4Hz、3.7Hz、3.9Hz。由于XD、YE、TT、TX 的參數基準值相對于DA、YH、YW來說較小,如果各個參數變化量都為1mm 時,相應的敏感度分析結果如圖3(b)所示,可以看出1T 切向模態與各個參數的敏感度從大到小依次為XD>TX>TT>YE>XK>YH>YW>YJ>θ>DA>XF。表5 為制動鼓模型中各個輸入變量分別增加1%時,1T~3T、2ND~11ND 共13 個模態輸出變量的增減量。綜合表5、圖3(b)以及實際幾何尺寸變化可行性可以看出,制動鼓的模態頻率對制動鼓幾何特征參數XF、YJ、YH、YW、θ及XK 的敏感度很小,即這幾個參數值對制動鼓的模態頻率影響相對較小。而制動鼓的外徑DA,帽蓋厚度TT、TX 以及最大外圈加強筋XD、YE 對對各階模態頻率的影響較大,尤其是能夠將6ND 與1T 及8ND 與2T 的模態隔離得更好。而且,DA、XD 對6ND 與1T 的模態影響是相反的。因此,可以通過優化這幾個參數將6ND 與1T 之間的模態隔離更大。在實際工作中,可以根據各階模態隔離的需求,對某一設計參數或某些組合設計參數進行優化來達到隔離模態的目的。例如:當帽蓋厚度TX增加0.5mm時,2T模態增加9.13Hz,而8ND 模態增加178.9Hz,因而8ND 與2T 的模態隔離從最初的223.9Hz 增加至393.67Hz。當帽蓋厚度TX 增加0.5mm同時使制動鼓外徑DA 減小2.46mm,可以使得8ND 與2T的模態隔離從原來的223.9Hz 增加到456.19Hz,而6ND 與1T 的模態隔離從241Hz 增加至311.46Hz。Note:
1.表中數據為設計變量增加1%時,反應變量的增減量。
2.表中括號內數值為制動鼓參數基準值。
3.2 制動鼓參數敏感度的驗證
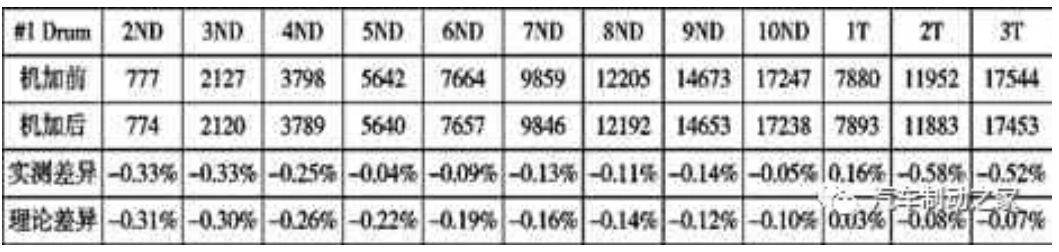
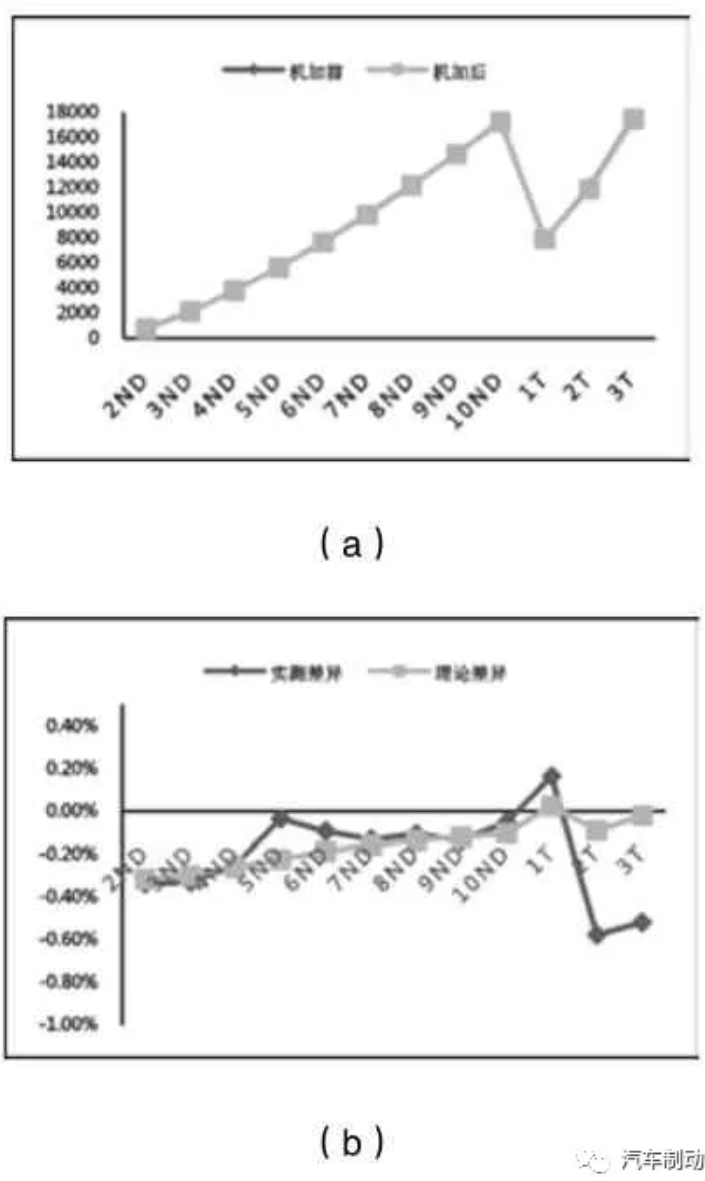
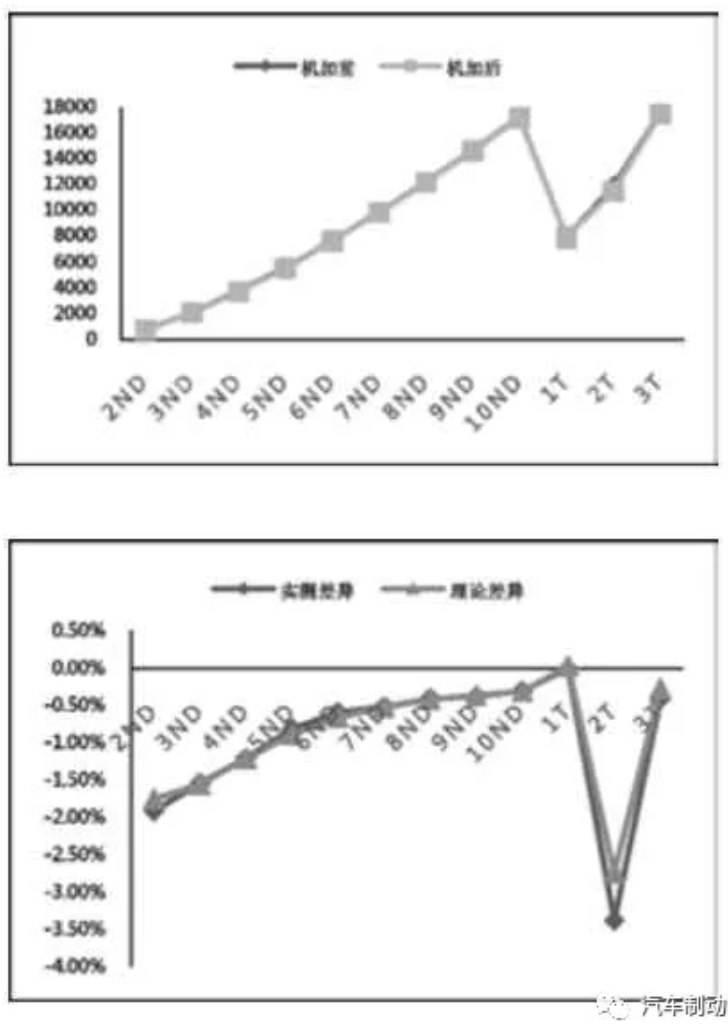
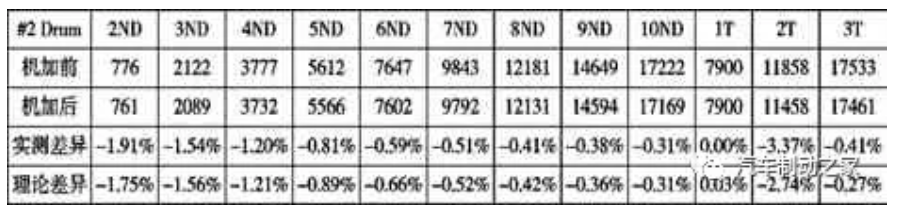
正為驗證制動鼓參數敏感度分析的可靠性,將制動鼓特征參數YE 和DA 分別按照如下進行機加:#1 號制動鼓YE減小1%(0.2mm),#2 號制動鼓YE 減小1%(0.2mm),同時DA 減小0.81%(2mm)。記錄機加之前及機加之后制動鼓各階模態,同時,將制動鼓的實測材料密度及彈性模量代入制動鼓參數化模型中進行修正,可得到修正后制動鼓模態頻率的理論差異。#1 號制動鼓的分析結果如表6 和圖4 所示,#2 號制動鼓的分析結果如表7 和圖5 所示。從表6 和圖4 可以看出,隨著1#制動鼓YE 尺寸的減小,各階ND 模態的實測值與理論值都呈減小趨勢,且ND 模態的實測差異與理論差異較為接近。而1T 實測模態同1T 理論模態呈變大趨勢,2T 與3T 的實測模態與理論模態呈減小趨勢,但2T 與3T 的實測模態差異比理論計算差異稍微偏大一些,最大差異都在0.58%以內。而且,從表6 分析可以看出6ND 與1T 的模態隔離從216Hz 增加至236Hz,而8ND 與2T 的模態隔離從原來的253Hz 增加到309Hz。從表7 和圖5 可以看出,當同時減小2#制動鼓的YE 和DA 尺寸時,各階ND 模態及T 模態的實測值與理論值都呈現減小趨勢,且整體模態的實測差異與理論差異的較為接近。而且,從表7 數據可以看出6ND 與1T 的模態隔離從253Hz增加至298Hz,而8ND 與2T 的模態隔離從原來的323Hz 增加到673Hz。基于上文分析可知,通過優化制動鼓的單一尺寸參數YE或者組合尺寸參數YE 和DA,可以有效地提高制動鼓的模態隔離結果,并說明該制動鼓參數化模型的敏感度分析具有較高可靠性。
4 結論
(1)利用ANSYS 對制動鼓進行參數化建模并對其模態進行試驗驗證,模態頻率誤差均小于1%,改參數化模型可靠性較好。(2) 通過對制動鼓模態與設計參數之間的敏感度研究,識別影響制動鼓模態隔離的關鍵因子:制動鼓的外徑、帽蓋厚度和最大外圈加強筋厚度。(3)基于參數敏感度分析結果,通過對關鍵因子進行優化分析,可快速解決制動鼓的模態隔離問題,有效縮短設計周期。
?